LIGHTGRID - Lichtnetz - REDDELUZ
lightgrid, St-Germain, gridwork, 7-Ray, Violet Ray, net-of-light
The vigesimal system - Mayan Numbers and their signs
The following post evolved as a reply toone of Peter Melchizedek's posts of the Star Codes he received, especially this Code:
Here is what I wrote:
I have just drawn the Twin Flame Encodement and noticed the severalr dots, feeling that each of them carries meaning - and also the exact position!
In Mayan mathematics dots stand for numbers - each dot being one number, thus counting up to four
. = 1
.. = 2
... = 3
.... = 4
Now, the interesting thing is that 5 is a line:
- = 5
O k- here are the basic numbers, as their system is vigesimal, these are the basic numbers:#
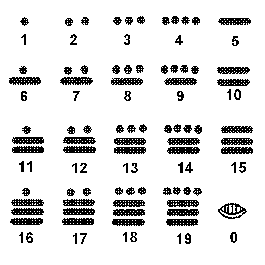
Note the similarity between the ZERO and the sign which you use for example in this encodement at both ends:

This is the sign for 20 - a dot and the ZERO:
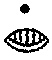
Here you see how it continues - the numbers from 1-29:

The POSITION of each dot and line MATTERS ... compare the number 6 to the number 25 - even the SPACE inbetween MATTERS ...

Two layers of signs are used to count up to 399 - as soon as there a three layers, we start from the number 400 = 20 x 20 x 1

To get a clue, you have to multiply each layer with the appropriate NUMBER, that is the bottom line is 1 the middle line is 20 and the third line on top is 400 ...


This system is NOT complicated once you understood it - or so they say, lol!
The only thing which IS complicated, especially in the beginning, is to relate it to our decimal system ...
The Maya were able to count everything with their fingers and toes - and show the numbers with hand signs.
The next layer of signs allowed the Maya to count from 8 000 to 159 999 - and the fifth layer of signs started out with 160 000 ... Three symbols - and so much MEANING! And all three symbols are in your star codes ...
That's it for now - here is the main link to the site from which I took the pictures. The descriptions are in German but I guess you can translate with google translator - or find an equivalent page in English.
http://www.labbe.de/zzzebra/index.asp?themaid=559&titelid=3254
There is only one more thing to mention, that is, when the Maya referred to calender Time, the third layer of signs was, according to the information on that site, equaled to 360 ...

I hope you enjoyed the journey through the NUMBERS of the vigesimal system of the Maya,
Sonja Myriel Aouine
Tags:
Replies to This Discussion
-
Permalink Reply by Myriel RAouine on February 29, 2012 at 5:57pm
-
THE MAYA MATHEMATICAL SYSTEM
The decimal mathematical system widely used today around the world in schools and accredited online MBA programs originated by counting with the fingers a person has. Counting with the fingers and toes started the Maya vigesimal system. So it is based on groups of twenty units. Just as the decimal system goes by 1, 10, 100, 1000, 10000, etc., the Maya vigesimal system goes 1, 20, 400, 8000, 160000, etc. While in the decimal system there are ten possible digits for each placeholder [0 - 9], in the Maya vigesimal system each placeholder has a possible twenty digits [0 - 19]. For example, in the decimal system 31 = 10 * 3 + 1 while in the vigesimal system 31 = 20 + 11. The Maya were masters of education and they discovered and used the zero. Their zero is represented by an ovular shell.
Characteristics of The Maya Mathematical System:
a) It is vigesimal, this means that it is based on 20 units [0 - 19] instead of the 10 units [0 - 9] of the decimal system. This table shows the first 20 numbers and their Arabic equivalents. Learn the Maya mathematical system fast using THE MAYA CALCULATION ASSISTANT. The Mayan names for numbers are here.
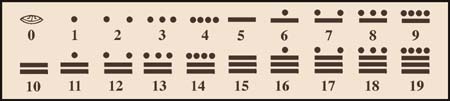
b) It only uses three symbols, alone or combined, to write any number. These are: the dot - worth 1 unit, the bar - worth 5 units and the zero simbolized by a shell.
c) It also uses a vigesimal positioning system, in which numbers in higher places grow multiplied by 20´s instead of the 10´s of the decimal system, compare number 168,421 in both systems:Place Number
168,421Place's
Decimal valueEquals & is
writtenPlace's
Vigesimal valueEquals & is
written6th 1 X 100,000= 100,000 3'200,000 5th 6 X 10,000 = 60,000 160,000 
4th 8 X 1,000 = 8,000 8,000 
3rd 4 X 100 = 400 400 
2nd 2 X 10 = 20 20 
1st 1 X 1 = 1 1 
TOTAL Arabic 168,421 Maya 168,421 d) Numbers in the Maya system can be written vertically or horizontally. In vertical writing, the bars are placed horizontally and the dots go on top of them, in this case the vigesimal positions grow up from the base. When written horizontally, the bars are placed vertically and the dots go to their left and higher vigesimal positions grow to the left of the first entry.




The Maya would write 168,421 (previous example) as: 
Thus when writing vertically the vigesimal positioning system, to write 20 a zero is placed in the first position (base) with a dot on top of it, in the second position. The dot in this place means one unit of the second order which equals to 20. To write 21, the zero would change to a dot (1 unit) and for the subsequent numbers the original 19 number count will follow in the first position. As they in turn reach 19 again another unit (dot) is added to the second position. Any number higher than 19 units in the second position is written using units of the third position. A unit of the third position is worth 400 (20 x 20), so to write 401 a dot goes in the first position, a zero in the second and a dot in the third. Positions higher than the third also grow multiplied by twenties from the previous ones. Examples of the numbers mentioned above follow:
(Note : the Maya made one exception to this order, only in their calendric calculations they gave the third position a value of 360 instead of 400, the higher positions though, are also multiplied by 20.)
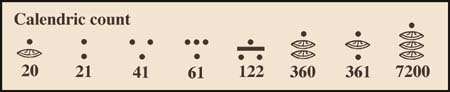
0 xix im 10 lahun 1 hun 11 buluc 20 hun kal 400 hun bak 2 caa 12 lahca 40 ca kal 800 ca bak 3 ox 13 oxlahun 60 ox kal 1200 ox bak 4 can 14 canlahun 80 can kal 1600 can bak 5 hoo 15 hoolahun 100 hoo kal 2000 hoo bak 6 uac 16 uaclahun 120 uac kal 8,000 pic 7 uuc 17 uuclahun 140 uuc kal 160,000 calab 8 uaxac 18 uaxaclahun 200 ka hoo kal 3'200,000 kinchil 9 bolon 19 bolonlahun 300 ox hoo kal 64,000,000 alau http://www.mayacalendar.com/mayamath.html -
-
Permalink Reply by Myriel RAouine on February 29, 2012 at 6:08pm
-
Mayan mathematics
American index History Topics Index Hernán Cortés, excited by stories of the lands which Columbus had recently discovered, sailed from Spain in 1505 landing in Hispaniola which is now Santo Domingo. After farming there for some years he sailed with Velázquez to conquer Cuba in 1511. He was twice elected major of Santiago then, on 18 February 1519, he sailed for the coast of Yucatán with a force of 11 ships, 508 soldiers, 100 sailors, and 16 horses. He landed at Tabasco on the northern coast of the Yucatán peninsular. He met with little resistance from the local population and they presented him with presents including twenty girls. He married Malinche, one of these girls.
The people of the Yucatán peninsular were descendants of the ancient Mayan civilisation which had been in decline from about 900 AD. It is the mathematical achievements of this civilisation which we are concerned with in this article. However, before describing these, we should note that Cortés went on to conquer the Aztec peoples of Mexico. He captured Tenochtitlán before the end of 1519 (the city was rebuilt as Mexico City in 1521) and the Aztec empire fell to Cortés before the end of 1521. Malinche, who acted as interpreter for Cortés, played an important role in his ventures.
In order to understand how knowledge of the Mayan people has reached us we must consider another Spanish character in this story, namely Diego de Landa. He joined the Franciscan Order in 1541 when about 17 years old and requested that he be sent to the New World as a missionary. Landa helped the Mayan peoples in the Yucatán peninsular and generally tried his best to protect them from their new Spanish masters. He visited the ruins of the great cities of the Mayan civilisation and learnt from the people about their customs and history.
However, despite being sympathetic to the Mayan people, Landa abhorred their religious practices. To the devote Christian that Landa was, the Mayan religion with its icons and the Mayan texts written in hieroglyphics appeared like the work of the devil. He ordered all Mayan idols be destroyed and all Mayan books be burned. Landa seems to have been surprised at the distress this caused the Mayans.
Nobody can quite understand Landa's feelings but perhaps he regretted his actions or perhaps he tried to justify them. Certainly what he then did was to write a book Relación de las cosas de Yucatán (1566) which describes the hieroglyphics, customs, temples, religious practices and history of the Mayans which his own actions had done so much to eradicate. The book was lost for many years but rediscovered in Madrid three hundred years later in 1869.
A small number of Mayan documents survived destruction by Landa. The most important are: the Dresden Codex now kept in the Sächsische Landesbibliothek Dresden; the Madrid Codex now kept in the American Museum in Madrid; and the Paris Codex now in the Bibliothèque nationale in Paris. The Dresden Codex is a treatise on astronomy, thought to have been copied in the eleventh century AD from an original document dating from the seventh or eighth centuries AD.

The Dresden codex:Knowledge of the Mayan civilisation has been greatly increased in the last thirty years (see for example [3] and [8]). Modern techniques such as high resolution radar images, aerial photography and satellite images have changed conceptions of the Maya civilisation. We are interested in the Classic Period of the Maya which spans the period 250 AD to 900 AD, but this classic period was built on top of a civilisation which had lived in the region from about 2000 BC.
The Maya of the Classic Period built large cities, around fifteen have been identified in the Yucatán peninsular, with recent estimates of the population of the city of Tikal in the Southern Lowlands being around 50000 at its peak. Tikal is probably the largest of the cities and recent studies have identified about 3000 separate constructions including temples, palaces, shrines, wood and thatch houses, terraces, causeways, plazas and huge reservoirs for storing rainwater. The rulers were astronomer priests who lived in the cities who controlled the people with their religious instructions. Farming with sophisticated raised fields and irrigation systems provided the food to support the population.
A common culture, calendar, and mythology held the civilisation together and astronomy played an important part in the religion which underlay the whole life of the people. Of course astronomy and calendar calculations require mathematics and indeed the Maya constructed a very sophisticated number system. We do not know the date of these mathematical achievements but it seems certain that when the system was devised it contained features which were more advanced than any other in the world at the time.
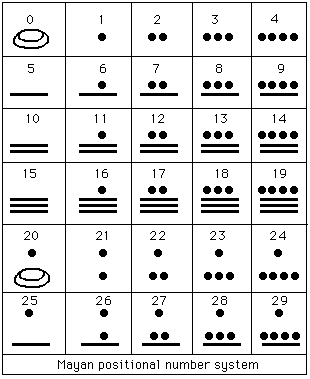
The Maya number system was a base twenty system.
Here are the Mayan numerals.Almost certainly the reason for base 20 arose from ancient people who counted on both their fingers and their toes. Although it was a base 20 system, called a vigesimal system, one can see how five plays a major role, again clearly relating to five fingers and toes. In fact it is worth noting that although the system is base 20 it only has three number symbols (perhaps the unit symbol arising from a pebble and the line symbol from a stick used in counting). Often people say how impossible it would be to have a number system to a large base since it would involve remembering so many special symbols. This shows how people are conditioned by the system they use and can only see variants of the number system in close analogy with the one with which they are familiar. Surprising and advanced features of the Mayan number system are the zero, denoted by a shell for reasons we cannot explain, and the positional nature of the system. However, the system was not a truly positional system as we shall now explain.
In a true base twenty system the first number would denote the number of units up to 19, the next would denote the number of 20's up to 19, the next the number of 400's up to 19, etc. However although the Maya number system starts this way with the units up to 19 and the 20's up to 19, it changes in the third place and this denotes the number of 360's up to 19 instead of the number of 400's. After this the system reverts to multiples of 20 so the fourth place is the number of 18 × 202, the next the number of 18 × 203 and so on. For example [ 8;14;3;1;12 ] represents
12 + 1 × 20 + 3 × 18 × 20 + 14 × 18 × 202 + 8 × 18 × 203 = 1253912.
As a second example [ 9;8;9;13;0 ] represents
0 + 13 × 20 + 9 × 18 × 20 + 8 × 18 × 202 + 9 × 18 × 203 =1357100.
Both these examples are found in the ruins of Mayan towns and we shall explain their significance below.
Now the system we have just described is used in the Dresden Codex and it is the only system for which we have any written evidence. In [4] Ifrah argues that the number system we have just introduced was the system of the Mayan priests and astronomers which they used for astronomical and calendar calculations. This is undoubtedly the case and that it was used in this way explains some of the irregularities in the system as we shall see below. It was the system used for calendars. However Ifrah also argues for a second truly base 20 system which would have been used by the merchants and was the number system which would also have been used in speech. This, he claims had a circle or dot (coming from a cocoa bean currency according to some, or a pebble used for counting according to others) as its unity, a horizontal bar for 5 and special symbols for 20, 400, 8000 etc. Ifrah writes [4]:-
Even though no trace of it remains, we can reasonably assume that the Maya had a number system of this kind, and that intermediate numbers were figured by repeating the signs as many times as was needed.
Let us say a little about the Maya calendar before returning to their number systems, for the calendar was behind the structure of the number system. Of course, there was also an influence in the other direction, and the base of the number system 20 played a major role in the structure of the calendar.
The Maya had two calendars. One of these was a ritual calendar, known as the Tzolkin, composed of 260 days. It contained 13 "months" of 20 days each, the months being named after 13 gods while the twenty days were numbered from 0 to 19. The second calendar was a 365-day civil calendar called the Haab. This calendar consisted of 18 months, named after agricultural or religious events, each with 20 days (again numbered 0 to 19) and a short "month" of only 5 days that was called the Wayeb. The Wayeb was considered an unlucky period and Landa wrote in his classic text that the Maya did not wash, comb their hair or do any hard work during these five days. Anyone born during these days would have bad luck and remain poor and unhappy all their lives.
Why then was the ritual calendar based on 260 days? This is a question to which we have no satisfactory answer. One suggestion is that since the Maya lived in the tropics the sun was directly overhead twice every year. Perhaps they measured 260 days and 105 days as the successive periods between the sun being directly overhead (the fact that this is true for the Yucatán peninsular cannot be taken to prove this theory). A second theory is that the Maya had 13 gods of the "upper world", and 20 was the number of a man, so giving each god a 20 day month gave a ritual calendar of 260 days.
At any rate having two calendars, one with 260 days and the other with 365 days, meant that the two would calendars would return to the same cycle after lcm(260, 365) = 18980 days. Now this is after 52 civil years (or 73 ritual years) and indeed the Maya had a sacred cycle consisting of 52 years. Another major player in the calendar was the planet Venus. The Mayan astronomers calculated its synodic period (after which it has returned to the same position) as 584 days. Now after only two of the 52 years cycles Venus will have made 65 revolutions and also be back to the same position. This remarkable coincidence would have meant great celebrations by the Maya every 104 years.
Now there was a third way that the Mayan people had of measuring time which was not strictly a calendar. It was an absolute timescale which was based on a creation date and time was measured forward from this. What date was the Mayan creation date? The date most often taken is 12 August 3113 BC but we should say straightaway that not all historians agree that this was the zero of this so-called "Long Count". Now one might expect that this measurement of time would either give the number of ritual calendar years since creation or the number of civil calendar years since creation. However it does neither.
The Long Count is based on a year of 360 days, or perhaps it is more accurate to say that it is just a count of days with then numbers represented in the Mayan number system. Now we see the probable reason for the departure of the number system from a true base 20 system. It was so that the system approximately represented years. Many inscriptions are found in the Mayan towns which give the date of erection in terms of this long count. Consider the two examples of Mayan numbers given above. The first
[ 8;14;3;1;12 ]
is the date given on a plate which came from the town of Tikal. It translates to
12 + 1 × 20 + 3 × 18 × 20 + 14 × 18 × 202 + 8 × 18 × 203
which is 1253912 days from the creation date of 12 August 3113 BC so the plate was carved in 320 AD.
The second example
[ 9;8;9;13;0 ]
is the completion date on a building in Palenque in Tabasco, near the landing site of Cortés. It translates to
0 + 13 × 20 + 9 × 18 × 20 + 8 × 18 × 202 + 9 × 18 × 203
which is 1357100 days from the creation date of 12 August 3113 BC so the building was completed in 603 AD.
We should note some properties (or more strictly non-properties) of the Mayan number system. The Mayans appear to have had no concept of a fraction but, as we shall see below, they were still able to make remarkably accurate astronomical measurements. Also since the Mayan numbers were not a true positional base 20 system, it fails to have the nice mathematical properties that we expect of a positional system. For example
[ 9;8;9;13;0 ] = 0 + 13 × 20 + 9 × 18 × 20 + 8 × 18 × 202 + 9 × 18 × 203 = 1357100
yet
[ 9;8;9;13 ] = 13 + 9 × 20 + 8 × 18 × 20 + 9 × 18 × 202 = 67873.
Moving all the numbers one place left would multiply the number by 20 in a true base 20 positional system yet 20 × 67873 = 1357460 which is not equal to 1357100. For when we multiple [ 9;8;9;13 ] by 20 we get 9 × 400 where in [ 9;8;9;13;0 ] we have 9 × 360.
We should also note that the Mayans almost certainly did not have methods of multiplication for their numbers and definitely did not use division of numbers. Yet the Mayan number system is certainly capable of being used for the operations of multiplication and division as the authors of [15] demonstrate.
Finally we should say a little about the Mayan advances in astronomy. Rodriguez writes in [19]:-
The Mayan concern for understanding the cycles of celestial bodies, particularly the Sun, the Moon and Venus, led them to accumulate a large set of highly accurate observations. An important aspect of their cosmology was the search for major cycles, in which the position of several objects repeated.
The Mayans carried out astronomical measurements with remarkable accuracy yet they had no instruments other than sticks. They used two sticks in the form of a cross, viewing astronomical objects through the right angle formed by the sticks. The Caracol building in Chichén Itza is thought by many to be a Mayan observatory. Many of the windows of the building are positioned to line up with significant lines of sight such as that of the setting sun on the spring equinox of 21 March and also certain lines of sight relating to the moon.

The Caracol building in Chichén Itza:With such crude instruments the Maya were able to calculate the length of the year to be 365.242 days (the modern value is 365.242198 days). Two further remarkable calculations are of the length of the lunar month. At Copán (now on the border between Honduras and Guatemala) the Mayan astronomers found that 149 lunar months lasted 4400 days. This gives 29.5302 days as the length of the lunar month. At Palenque in Tabasco they calculated that 81 lunar months lasted 2392 days. This gives 29.5308 days as the length of the lunar month. The modern value is 29.53059 days. Was this not a remarkable achievement?
There are, however, very few other mathematical achievements of the Maya. Groemer [14] describes seven types of frieze ornaments occurring on Mayan buildings from the period 600 AD to 900 AD in the Puuc region of the Yucatán. This area includes the ruins at Kabah and Labna. Groemer gives twenty-five illustrations of friezes which show Mayan inventiveness and geometric intuition in such architectural decorations.
References (26 books/articles)
Other Web sites:
- Kevin Brown (Mayan numeration)
- Rhonda Robinson (Mayan numbers)
- Mayan World Study Center (Mayan Mathematics)
- Mayan World Study Center (The Mayan calendar)
- Michiel Berger (Mayan Astronomy)
- B and V Böhm(The Dresden codex)
Article by: J J O'Connor and E F Robertson
-
Help us to anchor the energy of the New Age on Earth. Get inspired and set up a grid with the intention to help HEAL Mother Earth and all Her Beings from the wounds of the past and WEAVE a new net of living LIGHT all around the planet to help all life forms evolve into Unity Consciousness.
Ascension is not about leaving the world - it is about bringing HEAVEN down to EARTH!
We are the living BRIDGE between the worlds and dimensions, between HEAVEN AND EARTH. We are free to move in TIME and SPACE when we enter the SACRED SPACE of the Divine Chamber of the HEART where the ThreeFold Flame resides and the god given Divine Blueprint is waiting to be downloaded into our earth bodies.
The TIME to ACTIVATE our Light Body is NOW.
Love Light BLESSINGS,
Sonja Myriel RAouine
"About the Use of the Violet Flame"
I have to tell you that when you as a conscious disciple manage the Violet Flame, a parallel activity of the Violet Flame is initiated internally. This results in the vibrational awakening of your chakras. Therefore, each time when you use the gift of the Violet Flame you are asked not only to focalize your attention on what you want to transmute but also on the internal activity which takes place within yourself.
One of the consequences of the continual use of the Violet Flame is the accelerated awakening of all your chakras, you will, step by step, wake up in a different world from where you live now.
…
https://lightgrid.ning.com/group/lightgrid/forum/topics/lightgrid-tw...
Lightgrid CONNEXION Groups
This is the space for you to ORGANISE your personal connexion group, to look for likeminded people, to introduce yourSELF and say what you would like to contribute to the every expanding NET OF LIGHT around the world.
COMING TOGETHER
You have received clear guidance on a project,type of meditation, course of action to take? You are WELCOME to share here so we can start DREAMING and thus CREATING together!
Events
Blog Posts
Forgiveness Prayer & Invocation By Steven Hutchinson
Posted by Steve Hutchinson on November 23, 2025 at 4:03am 0 Comments 0 Likes
Divine Activities For Spiritual Growth By Steven Hutchinson
Posted by Steve Hutchinson on October 31, 2025 at 11:30am 0 Comments 0 Likes
Celestial Magic Invocation By Steven Hutchinson
Posted by Steve Hutchinson on September 10, 2025 at 3:26pm 0 Comments 0 Likes
Decree For Living By Steven Hutchinson
Posted by Steve Hutchinson on September 2, 2025 at 9:58am 0 Comments 0 Likes
Supreme Divine Freedom Decree By Steven Hutchinson
Posted by Steve Hutchinson on August 20, 2025 at 12:00am 0 Comments 0 Likes
Your Diamond Blue Light Decree By Steven Hutchinson
Posted by Steve Hutchinson on August 6, 2025 at 12:00pm 2 Comments 2 Likes
Videos
PHOTO Gallery
July 3rd-4th 2014 and March 20th-21st 2015:
ANCHORING the GOLDEN LIGHT FREQUENCY of CHRIST LOVE and CONSCIOUSNESS!
SUN and Central Sun Connection
Find more photos like this on LIGHTGRID - Lichtnetz - REDDELUZ
© 2025 Created by Steve Hutchinson.
Powered by
![]()